컴퓨터 프로그래밍의 예술 연습문제 1.1.7

11 Apr 2018

 

이 포스트에서는 컴퓨터 프로그래밍의 예술 1장 1절의 연습문제 7번에 대해서 분석해본 내용을 설명하겠습니다.

파트1

\(U_m\)에 대해 생각하기에 앞서 본문에서 소개되는 \(T_n\)에 대한 다음 명제에 대해 엄밀한 증명을 시도해본다.

\(m = 1\), \(m = 2\), …, \(m = n\) 이라는 유한한 집합에 대해 \(E1\)의 수행 횟수를 세고 그것을 \(n\)으로 나누면 \(T_n\)을 얻게 되는 것이다.

우선, \(m\)과 \(n\)이 주어졌을 때 \(m\)을 \(n\)으로 나눈 나머지가 \(r\)이라고 하자. 이 때, \(r \neq 0\) 이면 \(E1\)의 수행 횟수는 \(m = r\) 일 때의 \(E1\)의 수행 횟수와 같고, \(r = 0\) 이면 \(m = n\) 일 때와 같다. 즉, \(n\)으로 나눴을 때 나머지가 동일한 \(m\)들의 \(E1\) 수행 횟수는 서로 같다. 예를 들어, \(n = 3\) 이면 \(3\)으로 나눴을 때 나머지가 \(1\)인 \(m = 1\), \(m = 4\), \(m = 7\), \(m = 10\), … 의 \(E1\) 수행 횟수가 동일하고, 나머지가 \(2\)인 \(m = 2\), \(m = 5\), \(m = 8\), \(m = 11\), … 의 \(E1\) 수행 횟수가 동일하다. 이는 유클리드 알고리즘을 몇몇 작은 수들에 대해 노트에 직접 써 보면서 계산해보면 확인할 수 있다.

이제 \(n\)이 주어졌을 때 수열 \(b_l\)을 \(\{b_l:m=l\) 일 때 \(E1\)의 수행 횟수, \(1 \le l \le n\}\) 로 정의하고 수열 \(a_i\)를 \(n\)개의 양의 정수 \(b_1\), \(b_2\), …, \(b_n\) 이 반복되어 나타나는 수열이라고 하자. 예컨대, \(n = 5\) 일 때 \(b_l = \{2\), \(3\), \(4\), \(3\), \(1\}\) 이고 \(a_i = \{2\), \(3\), \(4\), \(3\), \(1\), \(2\), \(3\), \(4\), \(3\), \(1\), \(2\), \(3\), …\(\}\) 이다. 이렇게 하면 \(\{a_i:m=i\) 일 때 \(E1\)의 수행 횟수, \(i \ge 1\}\) 가 되어, 다음과 같이 문제를 정의할 수 있다.

문제

\(b_1\), \(b_2\), …, \(b_n\) 의 평균을 \(\alpha\)라 하자. 이제 수열 \(c_k\)를 \(a_i\)의 쳣 \(kn\)개의 원소, 즉, \(a_1\), \(a_2\), …, \(a_n\), \(a_{n+1}\), \(a_{n+2}\), …, \(a_{2n}\), \(a_{2n+1}\), \(a_{2n+2}\), …, \(a_{3n}\), …, \(a_{kn}\) 의 평균이라하면,

\[ c_k = \frac{1}{kn}\sum_{i=1}^{kn}a_i = \frac{1}{kn}k\sum_{l=1}^{n}b_l = \frac{1}{n}\sum_{l=1}^{n}b_l = \alpha \]

가 되어 \(c_k \to \alpha\) 이다. 이 때, 수열 \(d_i\)를 \(a_1\), \(a_2\), …, \(a_i\) 의 평균이라 하면 \(d_i \to \alpha\) 임을 보여라.

증명

\(p + 1\) 번째로 \(b_1\), \(b_2\), …, \(b_n\) 이 반복되는 구간에서 \(d_i\)를 구해보자. 즉, \(pn + 1 \le i \le (p+1)n\) 일 때 \(d_i\) 값을 구해보는 것이다. 이 때, \(a_{pn+1} = b_1\), \(a_{pn+2} = b_2\), …, \(a_{(p+1)n} = b_n\) 이고, 다음이 성립한다.

\[ d_i = \frac{\alpha pn + \sum_{l=1}^{i - pn}b_l}{i} = \frac{\alpha pn}{i} + \frac{\sum_{l=1}^{i - pn}b_l}{i} \]

\(\frac{\alpha pn}{i} = A\), \(\frac{\sum_{l=1}^{i - pn}b_l}{i} = B\) 라고 하면, \(pn\,\lt\,i\,\le\,(p+1)n\) 이고 \(b_l > 0\) 이므로

\[ \begin{align} \frac{\alpha pn}{(p+1)n} &\le A \lt \frac{\alpha pn}{pn}\newline \frac{p}{p + 1}\alpha &\le A \lt {\alpha} \end{align} \]

이고,

\[ B\le\frac{\sum_{l=1}^nb_l}{i}\lt\frac{\sum_{l=1}^nb_l}{pn}=\frac{\alpha}{p} \]

이다. 따라서, \((1 - \frac{1}{p+1})\alpha \le A + B \lt (1 + \frac{1}{p})\alpha\) 이고 \(\vert d_i-\alpha\vert \lt \frac{1}{p}\alpha\) 가 성립한다.

지금까지 우리는 \(pn + 1 \le i \le (p+1)n\) 임을 가정하였다. 이제 \(i \gt pn\) 일 때 \(\vert d_i-\alpha\vert \lt \frac{1}{p}\alpha\) 임을 알 수 있다. 왜냐하면, \(\hat p \gt p\) 인 \(\hat p\)에 대해, \(\hat pn + 1 \le i \le (\hat p+1)n\) 이면 \(\vert d_i-\alpha\vert \lt \frac{1}{\hat p}\alpha \lt \frac{1}{p}\alpha\) 이기 때문이다.

따라서, 임의의 \(\epsilon \gt 0\) 에 대해서 \(p = \lceil\frac{\alpha}{\epsilon}\rceil\), \(N = pn\) 이라고 하면, \(i\gt N\)일 때 \(\vert d_i-\alpha\vert \lt \frac{1}{\lceil\frac{\alpha}{\epsilon}\rceil}\alpha \le\frac{1}{\frac{\alpha}{\epsilon}}\alpha =\epsilon\) 이 되어서 \(d_i \to \alpha\) 이다. \(\blacksquare\)

다음은 \(b_l = \{2, 3, 4, 3, 1\}\) 일 때, \(d_i\) 값의 추이를 나타낸다.

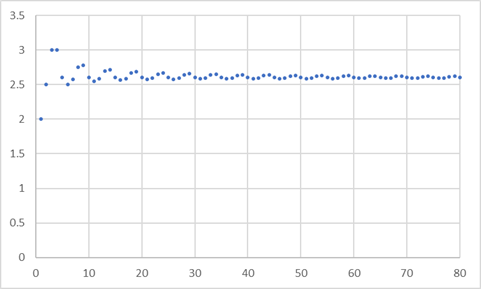
파트2

이제 \(U_m\)을 구해보자. \(m\)이 주어졌을 때 \(\{\hat a_i:n=i\) 일 때 \(E1\)의 수행 횟수, \(i \ge 1\}\) 라고 정의하면 \(\hat a_i = \{r_1\), \(r_2\), …, \(r_m\), \(b_1+1\), \(b_2+1\), …, \(b_m+1\), \(b_1+1\), \(b_2+1\), …, \(b_m+1\), \(b_1+1\), \(b_2+1\), …\(\}\) 이 된다\((r_l\)은 상수값으로 정해진다\()\). \(a_i\)와 \(\hat a_i\)을 비교해보면, 앞 부분에 유한개의 원소만 다르고 그 이후의 원소들은 모두 \(\hat a_i\)이 \(1\)씩 크기 때문에, \(\hat a_i\)의 평균은 \(a_i\)의 평균보다 \(1\)이 더 큰 값으로 수렴할 것이다. 이를 수식을 통해 확인해 보려면 다음과 같이 문제를 정의할 수 있다.

문제

\(\hat d_i\)를 \(\hat a_1\), \(\hat a_2\), …, \(\hat a_i\) 의 평균이라 하면 \(\hat d_i \to \alpha + 1\) 임을 보여라.

증명

\(i \gt m\) 인 경우,

\[ \hat d_i = \frac{\sum_{l=1}^mr_l + d_{i-m}(i-m) + (i-m)}{i} \]

이 되어 \(\lim_{i \to \infty}\hat d_i = \lim_{i \to \infty}(d_{i-m} + 1) = \alpha + 1\) 이다. \(\blacksquare\)